ICFP Programming Contest 2018

— 23 October 2018 —

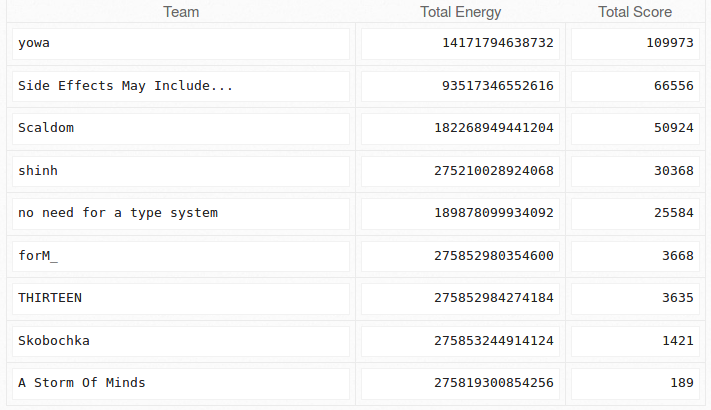
In July, I participated together with a friend of mine, Achilles Benetopoulos, in the ICFP programming contest. Our team name was “no need for a type system” because we implemented our solution in Erlang (which has a type system, though not a static one) and at the time (after programming for “a couple” of hours straight) it seemed like a very entertaining name. On the lightning round we managed to rank on the 10th place (which was surprisingly higher than our expectations).

Our final rank

In this article, I will try to describe the experience of my team during the lightning round of the ICFP 2018 programming contest, the solution that we submitted, and general ideas and notes that came up during and after the contest. Our solution is certainly not the best for the specific problem, but I believe that there is benefit in documenting the whole process.

The full code of our submission can be found at this repo.

Lightning round problem overview

Here is a brief overview of the problem. We have a fleet of 3D printing nanobots that operate in time steps. Each nanobot can either move, wait, spawn another nanobot, or print a voxel in a 3D space, and they are each commanded by a sequence of instructions. However, the nanobots need energy to be operated, and their energy consumption depends on many factors, such as the number of time steps that they are operating for. We are given a 3D sculpture, whose size is bounded by R in each dimension (R ranges from 1 to 250), and we want to generate a sequence of instructions for each nanobot, that minimizes the total energy that is consumed.

The detailed problem description can be found here for anyone that is interested.

System frequency

Before describing the different nanobot commands, it is essential to state that the 3D printing nanobot system can be in one of two states at any time, low or high frequency. The difference between those states in practice is whether “floating” voxels can be 3D printed or not. If the system is in “low-frequency” only voxels in contact with grounded voxels can be printed. Otherwise, voxels can be printed anywhere, even if they are not in contact with grounded voxels. Grounded voxels are recursively defined as voxels which are in contact with the ground level (Their y-coordinate is zero) or are in contact with a grounded voxel.

Nanobot commands

There are 8 nanobot commands supported by the system.

Energy costs

There are five ways in which energy is consumed during the execution of the system.

The energy cost associated with printing a voxel cannot be reduced, as all voxels of the sculpture must be printed. In addition the energy cost of spawning new nanobots is negligible because combining two nanobots (with the fusion command) returns that energy to the system.

Thus the main costs are the first three, with the first one dominating when R is large enough. If we have 20 nanobots, which is the maximum possible number of nanobots, all making the longest possible move at the same time step, the amount of energy that will be consumed is 1000 which is less than the total system energy consumption for one time step even when R >= 10. In addition, having the system in “low frequency” seemingly saves a lot of energy, but constrains parallelism a lot, as being in low frequency requires that voxels are printedfrom the ground up.

Because of the above, we decided to focus on minimizing the total number of time steps that the system runs, without initially caring about keeping the system in “low-frequency”.

First naive solution to the problem

Instead of just giving our solution to the problem, I will first try to describe our approach and how this led us to our first naive solution.

The solution that the problem requires is analogous to a compiler which transforms a high level specification (the target 3D sculpture) to a program, that when executed, produces this 3D structure.

Having this view, we first tried to implement the simplest (and therefore completely inefficient) correct program that produces this 3D sculpture. That is, a single nanobot that “scans” the entire 3D space voxel by voxel, and prints the target voxels. Our nanobot traverses space from the lowest to the highest xz plane, and in each plane from the left to the right line by line. Every time it finishes with a line, it moves to the beginning of the next line and starts again. Each time it finishes with a whole plane, it goes to the beginning of the next plane and starts again.

Of course this solution is completely inefficient, however it acted as a great foundation, to incrementally add optimization passes to the generated programs, thus improving their efficiency.

There are two main optimization directions, one is improving the sequential performance of each nanobot, and the other is utilizing more nanobots to parallelize the computation, as the largest energy overhead is caused by the number of rounds that the program is executed. A separate section is dedicated to each optimization direction.

Sequential Optimizations

In theory, an optimal sequential strategy would visit the voxels that a nanobot needs to print with the goal of minimizing the movement (both in distance and in rounds) that the nanobot needs to do. Well this problem sounds familiar (TSP) and we decided that it was not a feasible solution to the problem. At that time we also thought that a solution like this could introduce a lot of crashes of a robot with the already produced voxels1.In retrospect, it seems like if a nanobot is going to crash to a voxel at round r2 that was already produced by itself at round r1, it means that it could have delayed printing this voxel until the round r2 as it would pass from there a second time. Thus if a nanobot prints all voxels at the latest possible time, then it will never crash with voxels created by itself. However this does not hold when many robots are printing voxels concurrently. Based on the above, we decided to go for a greedier approach.

As I also mentioned before, in our naive solution a nanobot traverses the whole 3D space and for every voxel that it passes, it checks whether it should print it or not as follows:

print_voxel(R, X, Y, Z, Model) when Z =:= R ->
  [{smove, [{1, 0, 0}]}] ++ return(z, R, Z) ++ 
  print_voxel(R, X + 1, Y, 2, Model);
print_voxel(R, X, Y, Z, Model) when X =:= R ->
  [{smove, [{0, 1, 0}]}] ++ return(x, R, X) ++ 
  print_voxel(R, 1, Y + 1, Z, Model);
print_voxel(R, X, Y, Z, Model) when Y =:= R ->
  return(y, R, Y) ++ [{smove, [{0,0,-1}]}];
print_voxel(R, X, Y, Z, Model) ->
  Fill =
    case nth(Z-1, nth(Y, nth(X, Model))) of
      0 -> [];
      1 -> [{fill, [{0,0,-1}]}]
    end,
  Move = [{smove, [{0,0,1}]}],
  Fill ++ Move ++ print_voxel(R, X, Y, Z+1, Model).

The nanobot moves on a z-axis line, until it reaches the end of the space, where it moves to the next line (by incrementing x) and then moves back to the start of the z-axis (with the return(z, R, Z) call). When it reached the end of the x-axis, it moves one plane up (by incrementing y), and it goes to the start of the x and z axes.

Based on that naive solution, the first optimization that we performed was to shorten the path of each nanobot, by implementing a back and forth movement, instead of having to return to the start of the z-axis everytime the nanobot reached the end of the line. The new print_voxel looks like this:

print_voxel(Min={_,_,MinZ}, Max={_,_,MaxZ}, Curr={X,Y,Z}, plus, Model, Acc) when Z > MaxZ ->
  NewAcc = [{smove, [{1, 0, 0}]}|Acc],
  print_voxel(Min, Max, {X + 1, Y, Z}, minus, Model, NewAcc);
print_voxel(Min={_,_,MinZ}, Max={_,_,MaxZ}, Curr={X,Y,Z}, minus, Model, Acc) when Z < MinZ ->
  NewAcc = [{smove, [{1, 0, 0}]}|Acc],
  print_voxel(Min, Max, {X + 1, Y, Z}, plus, Model, NewAcc);
print_voxel(Min={MinX,_,MinZ}, Max={MaxX,_,MaxZ}, Curr={X,Y,Z}, Direction, Model, Acc) when X > MaxX ->
  MoveToStart = 
    lists:flatten([move_robot({X, Y, Z}, {X, Y, MinZ - 1}), 
                   move_robot({X, Y, MinZ - 1}, {MinX - 1, Y, MinZ - 1})]),
  {lists:reverse(Acc) ++ MoveToStart, {MinX-1,Y,MinZ-1}};
print_voxel(Min, Max, {X, Y, Z}, Direction, Model, Acc) ->
  {Move, NewZ} = 
    case Direction of
      plus -> {[{smove, [{0,0,1}]}], Z + 1};
      minus -> {[{smove, [{0,0,-1}]}], Z - 1}
    end,
  {Lookup, ToFill} = 
    case Direction of
      plus -> { {X,Y,NewZ - 1}, {0, 0, -1}};
      minus -> { {X,Y,NewZ + 1}, {0, 0, 1}}
    end,
  Fill =
    case model_get(Lookup, Model) of
      0 -> [];
      1 -> [{fill, [ToFill]}]
    end,
  NewAcc = Fill ++ Move ++ Acc,
  print_voxel(Min, Max, {X, Y, NewZ}, Direction, Model, NewAcc).

The second optimization that we performed was bounding the movement of a nanobot by the bounding box of the sculpture on each plane. By doing that a nanobot does not need to scan space where there is no voxel to be printed.

The third was the most important sequential optimization that we performed. The generated sequence of commands for a nanobot, contains a lot of unecessary 1 voxel moves, as the nanobot scans the whole space voxel by voxel. However, we are allowed to move a nanobot up to 15 voxels away with a single one axis move command, or up to 5 voxels in 2 axes. This means that a lot of energy can be conserved, by merging all those 1 voxel move instructions to longer move instructions, as the total execution time would drastically reduce.

This is the code that performs this optimization:

optimize_seq_trace(Commands) ->
  optimize_seq_trace(Commands, {0,0,0}, []).

optimize_seq_trace([], Buffer, Acc) ->
  FinalMoves = instantiate_moves(Buffer),
  lists:reverse(Acc) ++ FinalMoves;
optimize_seq_trace([Com|Commands], Buffer, Acc) ->
  case Com of
    {smove, [Cd]} ->
      optimize_seq_trace(Commands, add_coords(Cd, Buffer), Acc);
    {lmove, [Cd1, Cd2]} ->
      optimize_seq_trace(Commands, add_coords(Cd2, add_coords(Cd1, Buffer)), Acc);
    _ ->
      BufferMoves = instantiate_moves(Buffer),
      NewAcc = [Com|lists:reverse(BufferMoves)] ++ Acc,
      optimize_seq_trace(Commands, {0,0,0}, NewAcc)
  end.

It doesn’t only merge consecutive small move instructions into longer ones, but it also removes opposite move commands by collecting all of the consecutive move instructions in a buffer, and then instantiating them with the least amount of commands whenever a non move command is encountered2.Looking back, it seems like merging consecutive move commands, “includes” the bounding box optimization, as all the moves outside of the bounding box would be merged into the least possible amount of moves to reach the bounding box.

Parallel Optimizations

The second optimization direction is increasing the number of nanobots, so that they can print voxels in parallel, thus reducing the total system execution time. However, this introduces new challenges as two nanobots cannot move through the same space during a time step, and nanobots can crash if they try to move through an already printed voxel. Because of that, parallelization should be guided by a strategy that avoids any interference between nanobots and voxels.

We tried to achieve that “orchestrated” parallelization by partitioning the space in levels based on height, and by assigning a set of those levels to each nanobot in a static fashion (later on we improved this static level assignment by assigning a level to a nanobot only after it is done with its previously assigned level, thus reducing the nanobot idle time).

By having the space partitioned in levels, we can still use the sequential printing algorithm and optimizations that we implemented before without any changes. Moreover, nanobots can never crash with already printed voxels or with each other when they both move horizontally, and interference is limited between two nanobots when at least one nanobot is transitioning in a vertical manner.

In order to eliminate this “vertical” intereference, we constrained parallelization in the following way. Each nanobot is allowed to move up and down between different levels on a vertical line that is unique to itself. This way we eliminate interference when both nanobots move vertically3.This is actually the worst type of interference, as it cannot be solved by stalling, but needs a more complicated interference elimination strategy (which gets even more complicated when more than 2 nanobots intefere at the same time step), where one nanobot has to temporarily move to the side, allowing the other nanobot to move, and then return back to its original position to proceed with its move.

Finally, we created an interference checker, which also contains an interpreter of nanobot programs, that executes all nanobot commands in parallel and checks for any possible interference between all pairs of nanobots. When an interference is detected, a Wait instruction is inserted to the vertically moving nanobots’ programs, in order to allow any interfering horizontally moving nanobots to complete their moves. It is important to note, that this simplistic collision avoidance algorithm wouldn’t work in situations where two nanobots try to move on the opposite (or the same) direction through the same line.

Discussion

In total, our solution was decent but I believe that there were some mistakes in our approach that we could learn from in the future.

First of all, the way we parallelized our solution felt “ultra-hacky” and not well thought out, as we never seriously considered its correctness during the contest. Our interference elimination algorithm is not general enough, and does not work for all corner cases. Consequently, during the final hours of the contest, we failed really hard when we tried to refine the parallelism strategy to a finer-grain by assigning sections of horizontal levels to each nanobot (instead of the whole level). In retrospect, the nanobot 3D printing system looks very similar to a multi-process concurrent system where processes compete in getting hold of specific resources (where processes are nanobots and resources are sections of the 3D space). Based on that, we could have searched for, and applied a much more sophisticated (and provably correct) analysis in order to eliminate interference as there exists a lot of relative work in the field of concurrent systems.

In addition, we shouldn’t have handled all testcases with the same algorithm, as the smaller (and less dense) sculptures could be printed with much less energy by keeping the system in “low-frequency” and only printing the closest grounded voxel in every timestep. This could have improved our score in a lot of the smaller testcases.

On the contrary, a final positive note is that I was surprised by how fast we managed to get the first naive implementation up and running. After reading and understanding the problem description, we agreed on the interface for the parse module, the output module, and the state representation and we set out to separately implement each part. This allowed us to completely parallelize the “dirty” initial process, and have a working ultra naive solution in about 3 hours after the beginning of the competition. (The following screenshot was taken when we succesfully managed to run our solution for the first time and we realised that despite being ultra naive it returned a reasonable first result.)

Our rank after about 3 hours

Hosted on GitHub Pages — Theme by orderedlist